About me
I am Eloi Martinet, a postdoctoral researcher at the University of Würzburg and part of the team of Mathematics of Machine Learning. I am interested in using a variational approach to tackle machine learning problems, and using neural networks capabilities to solve shape optimization problems.
In October 2023, I defended my PhD Thesis about spectral shape optimization supervised by Dorin BUCUR and Edouard OUDET. You can download the manuscript here.
You can download my CV here.
Education
-
Postdoc in Variational Methods in Machine Learning.
JMU (Würzburg, Germany) -
PhD in Spectral Shape Optimization, 2019-2023
LAMA (Chambéry), LJK (Grenoble) -
Agrégation de Mathématiques, 2020-2021
Institut Fourier (Grenoble) -
Engineering School in Informatics and Applied Mathematics, 2016-2019
ENSIMAG (Grenoble)
Research interests
- Shape and topology optimization
- Numerical methods for PDEs
- Level set method
- Neural Networks
- Graph-based Machine Learning
Teaching
- 2025 : Lab of Machine Learning, JMU (Würzburg)
- 2025 : Working Group on FEM and the use of Neural Networks as PDE solver, JMU (Würzburg)
- 2024-2025 : Lectures and exercise session of Mathematical Foundations of Data Science, JMU (Würzburg)
- 2024-2025 : Seminar of Introduction to Data Science, JMU (Würzburg)
- 2024 : Seminar of Machine Learning on Graphs, JMU (Würzburg)
- 2024 : Working Group on FEM and the use of Neural Networks as PDE solver, JMU (Würzburg)
- 2022 - 2023 : tutoring of practical sessions of numerical analysis, ENSIMAG (Grenoble)
- 2022 - 2023 : tutoring of practical sessions of integration and Fourier transform, ENSIMAG (Grenoble)
- 2021 - 2022 : course + tutoring of practical sessions of basic analysis, UGA (Grenoble)
- 2019 - 2020 : tutoring of practical sessions of numerical analysis, USMB (Chambery)
Supervision
- 2025 : Co-supervison of the MSc Internship of Nick Burk with Leon Bungert about Phase Field on Graphs.
- 2024 : Co-supervison of the MSc Internship of Nicolas Roblet with Romain Joly titled Spectrum of unbounded operators and applications to PDEs (report).
Publications
& preprints-
Spherical caps do not always maximize Neumann eigenvalues on the sphere
(2025),
with D. BUCUR, R.S. LAUGESEN and M. NAHON, Preprint. -
Meshless Shape Optimization using Neural Networks and Partial Differential Equations on Graphs
(2025),
with L. BUNGERT, Scale Space and Variational Methods in Computer Vision (to appear). -
Sharp inequalities for Neumann eigenvalues on the sphere
(2024),
with D. BUCUR and M. NAHON, Journal of Differential Geometry (to appear). -
Numerical optimization of Neumann eigenvalues of domains in the sphere
(2024),
Journal of Computational Physics. -
Maximization of Neumann eigenvalues
(2023),
with D. BUCUR and E. OUDET, Archive for Rational Mechanics and Analysis.
Research Projects
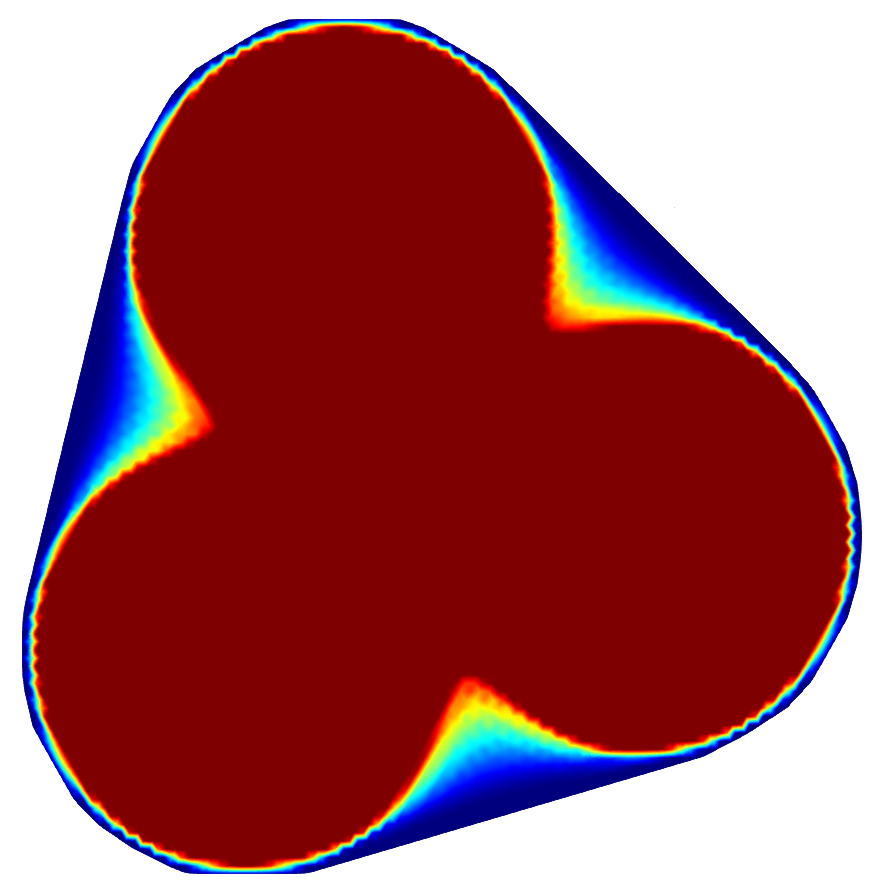
Optimization of Neumann eigenvalues in the plane
What is the shape of the drum that has the largest eigenfrencies ? We investigate this issue by implementing some density-based optimization procedure.
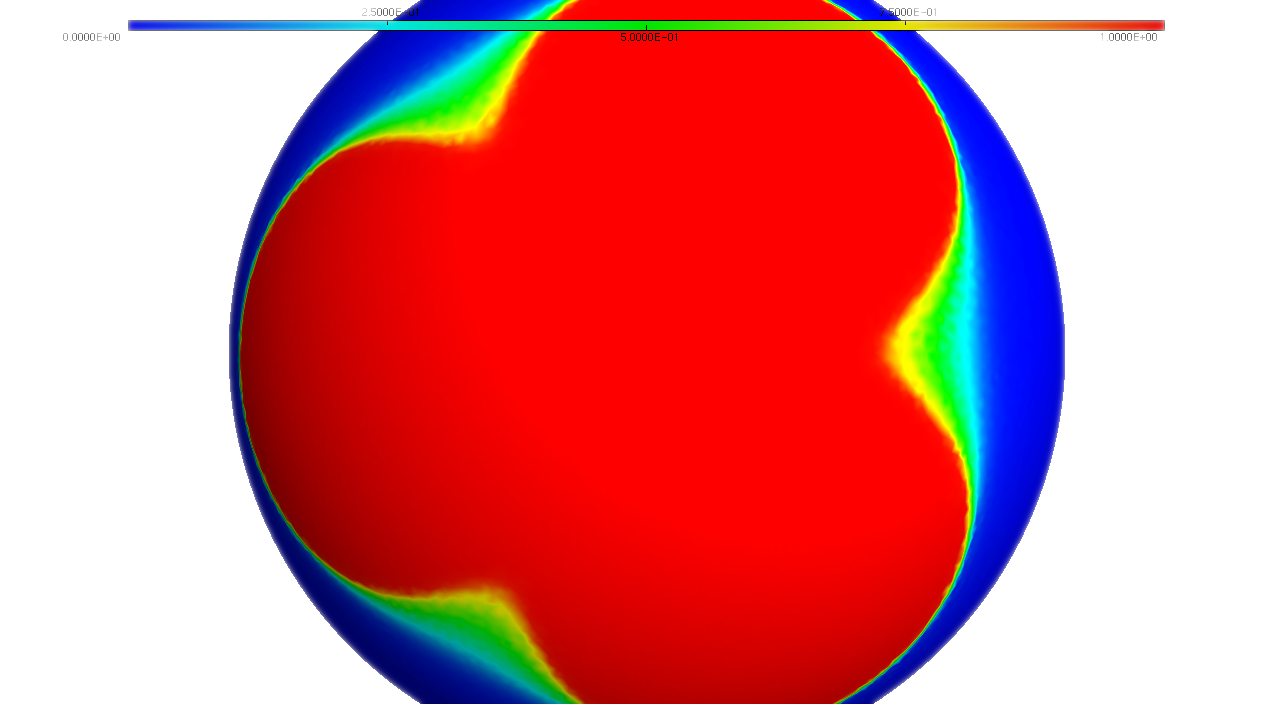
Density optimization of Neumann eigenvalues on the sphere
While the planar case has been investigated theoretically since the 50's, the optimization of Neumann eigenvalues on the sphere is still mysterious. We try to identify numerically some behaviour of the optimal densities.
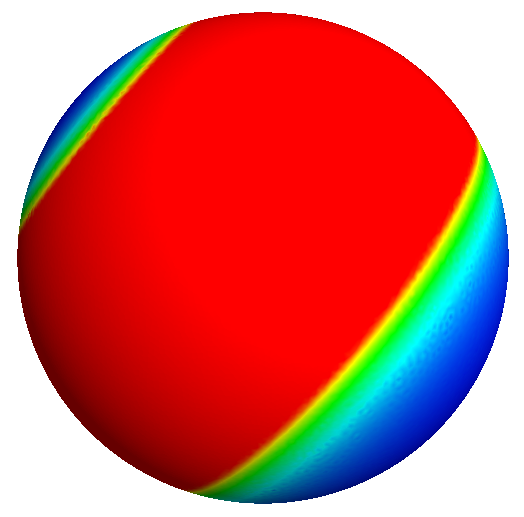

Level set optimization of Neumann eigenvalues on the sphere
We perfom an analysis of the shape optimization problem of Neumann eigenvalues for domains on the sphere thanks to the level set method.
Solving PDEs with Graphs
Originally used in the context of unsupervised and semi-supervised learning, the graph laplacian can also be used as as a numerical PDE solver.


Neural-network-based level set method
Parametrizing a level set function with a neural network proved to be useful for overcoming certain burdens of mesh-based level set methods and computing easily common geometric quantities.
Teaching ressources

Numerical Methods for PDEs
From the Finite Element Method to Neural Networks
Exploring old and recent ways to solve PDEs. Given at the University of Würzburg in the summer semester of 2024.
Go to the courseOther Projects
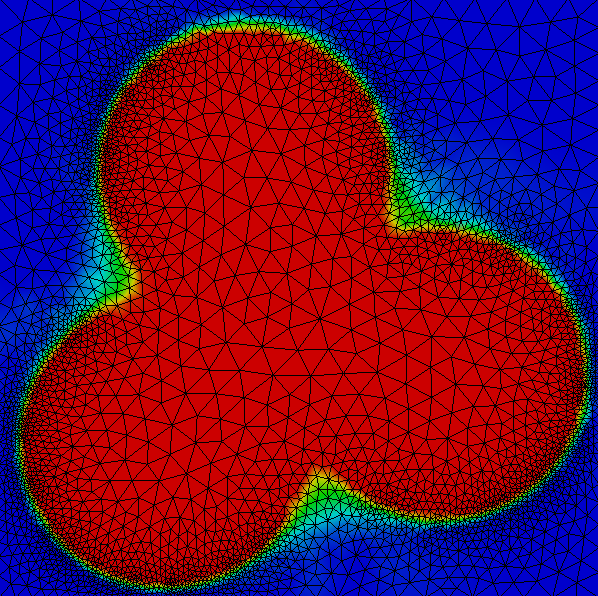
Optimization of Neumann eigenvalues with FreeFem and Python
I provide the source code and some practical explanations on the density optimization of Neumann eigenvalues using python and FreeFem++.
A phase-field demonstration of the isoperimetric problem
The legendary isoperimetric problem is the most famous and ancient problem in shape optimization. It consists in finding the shape minimizing its perimeter while keeping its volume fixed. Here we simulate the solution to this problem using a relaxed formulation of the perimeter.

Image segmentation using Semi Supervised Learning
A notebook developed in the context of an outreach activity at the University of Würzburg. It shows how to perform semi-supervised segmentation using a graph approach.
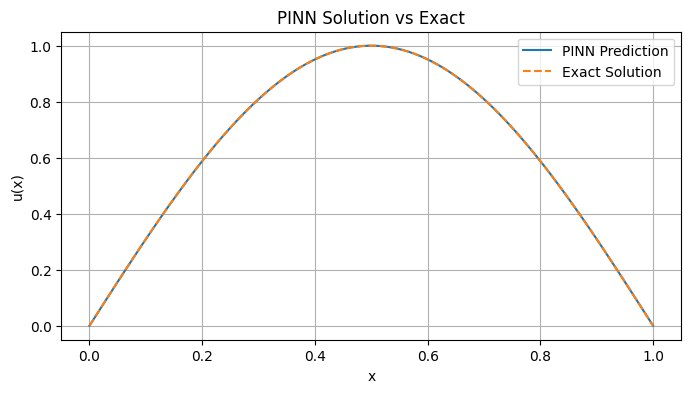
Solving PDEs with neural networks
A folder of notebooks used in the context of my lecture on FEM and PINNs, showing different methods to solve PDEs with neural networks: PINNs, DRM, Natural Gradient Descent and Sampled Neural Networks.