Presentation of the problem
Here are some results obtained during the first part of my thesis in collaboration with Dorin Bucur and Edouard Oudet. We are interested in the following problem : Let $\Omega \subset \mathbb{R}^N$, $N \geq 1$ be an open set with Lipschitz boundary. Then there exists a sequence $$ 0 = \mu_0(\Omega) \leq \mu_1(\Omega) \leq ... \to \infty $$ such that $$ \begin{cases} -\Delta u = \mu_k(\Omega) u \mbox { in } \Omega,\\ \frac{\partial u}{\partial n} = 0 \mbox { on } \partial \Omega, \end{cases} $$ for some $u \in H^1(\Omega) \setminus \{0\}$ . The $\mu_k(\Omega)$ are called the eigenvalues of the Laplace operator with Neumann boundary conditions and the associated $u$ is called an eigenfunction. It can be seen as the way a membrane vibrates when it isn't fixed at its boundary. The question we are considering is then, for a given $k \in \mathbb{N}$ and a given volume $m > 0$ to find the domain $\Omega$ which maximizes the eigenvalue $\mu_k(\Omega)$ with $|\Omega| = m$ $$ \max \left\{ \mu_k(\Omega) : \Omega \subset \mathbb{R}^N, |\Omega| =m\right\}. $$ The well knows Courant-Hilbert formula allows us to express the eigenvalues in the following manner : $$ \mu_k(\Omega) = \min_{S\in{\mathcal S}_{k+1}} \max_{u \in S\setminus \{0\}} \frac{\int_\Omega |\nabla u|^2 dx}{\int_\Omega u^2 dx}, $$ where ${\mathcal S}_k$ is the family of all subspaces of dimension $k$ in $H^1(\Omega)$.
Extension to densities
Since really few is known on this problem, we aimed at considering a broader problem: let $\rho : \mathbb{R}^N \to [0,1]$ such that $0<\int_{\mathbb{R}^N} \rho dx <+\infty$. We consider the degenerate eigenvalue $$ \mu _k(\rho) := \inf_{S\in{\mathcal S}_{k+1}} \max_{u \in S} \frac{\int_{\mathbb{R}^N} \rho|\nabla u|^2 dx}{\int_{\mathbb{R}^N} \rho u^2 dx}, $$ where ${\mathcal S}_{k+1}$ is the family of all subspaces of dimension $k+1$ in $$ \{u\cdot 1_{\{\rho (x)>0\}}: u \in C^\infty_c (\mathbb{R}^N)\}. $$
Numerical approximation of optimal densities
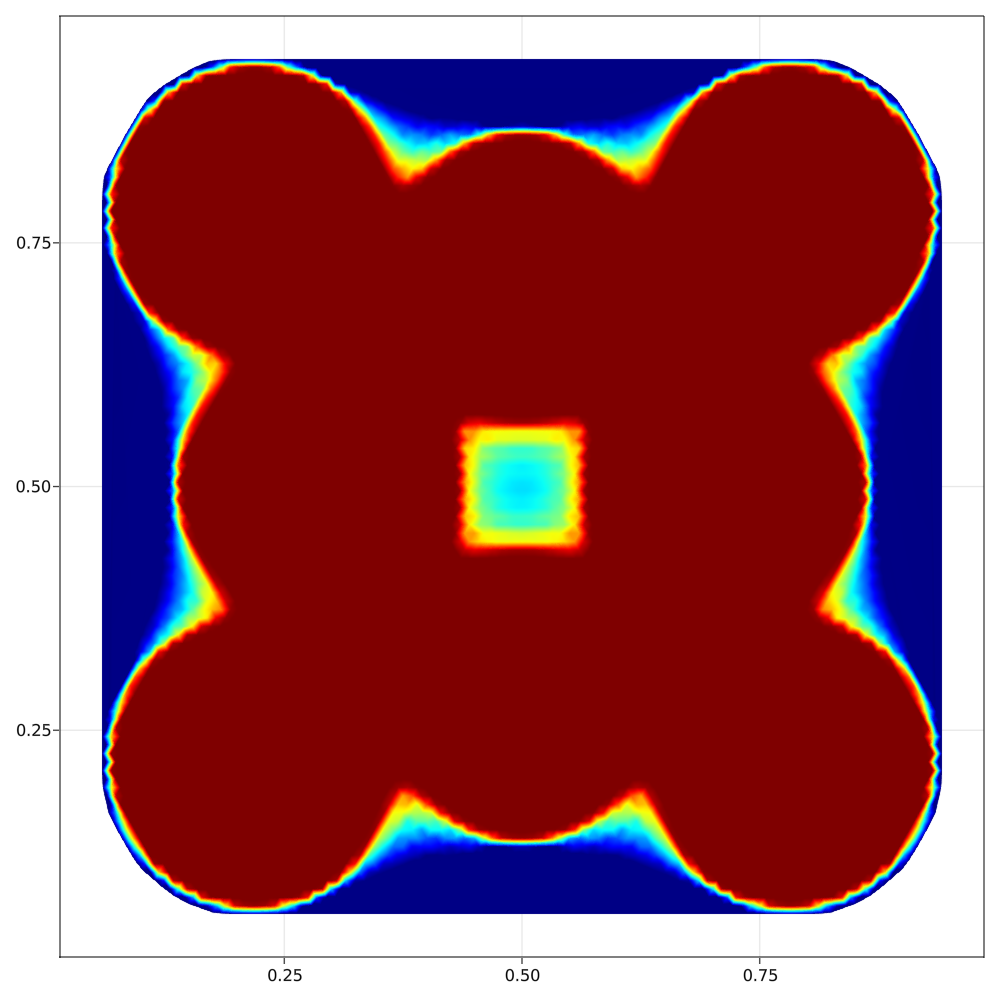
Using some gradient-based algorithm, we are able to illustrate the optimal density $\rho$ for a given $k \in \mathbb{N}$. We illustrate the convergence of the algorithm in the following figures, representing the optimization process of the eigenvalues for $k=1,...4$.
Final results
After some post-processing, we can finally compute the approximate optimal density for $k=1,...8$ :


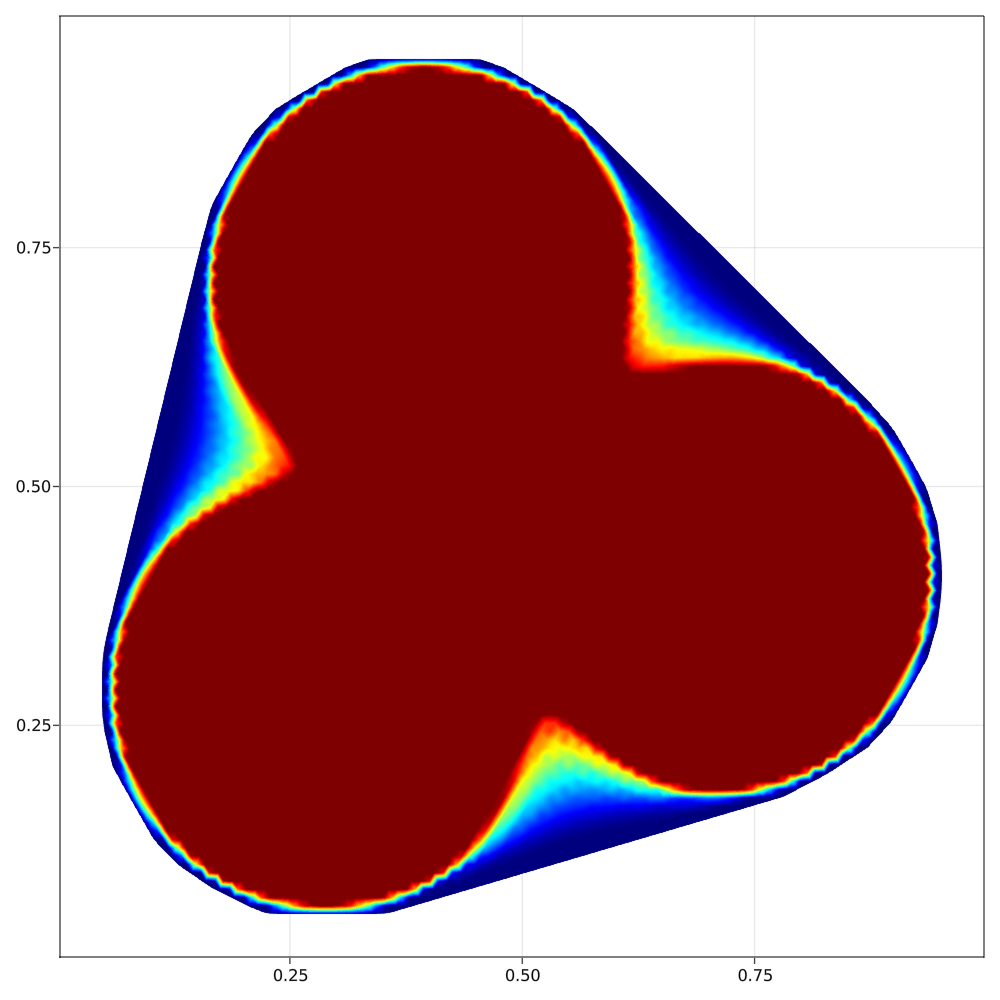
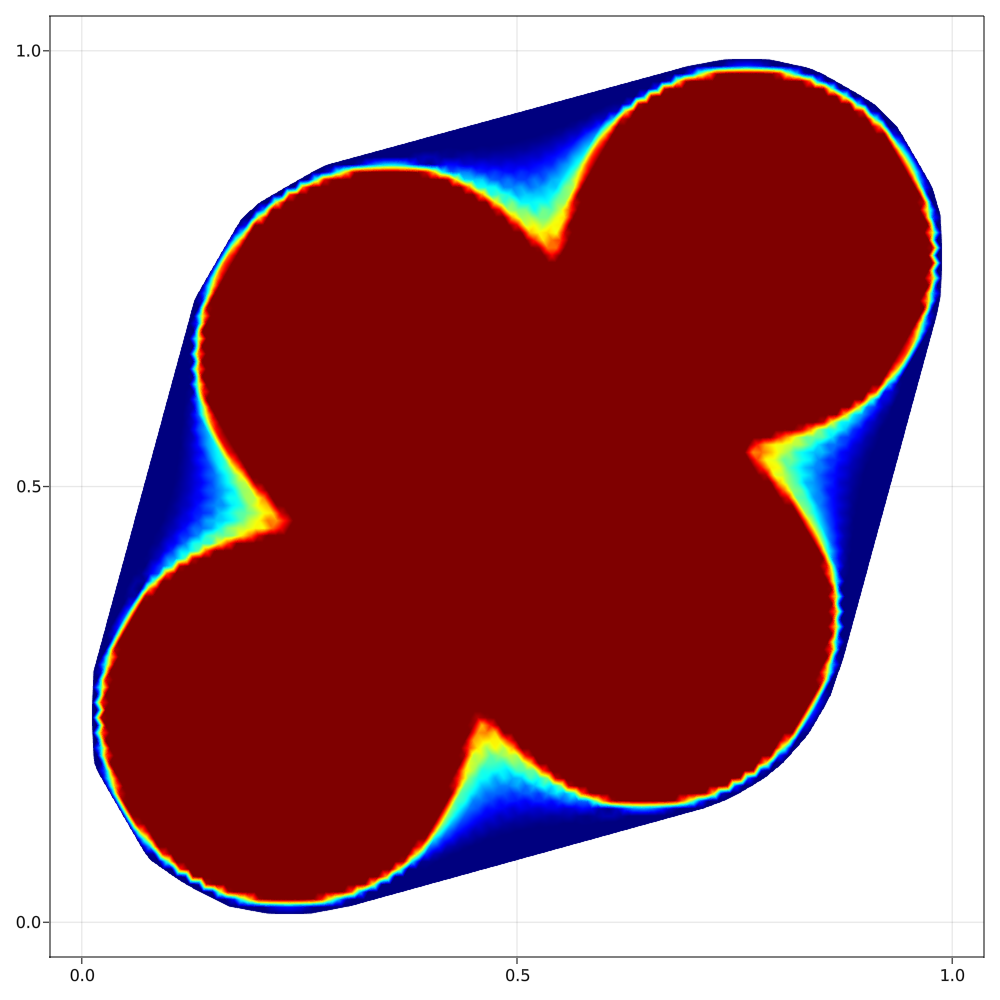
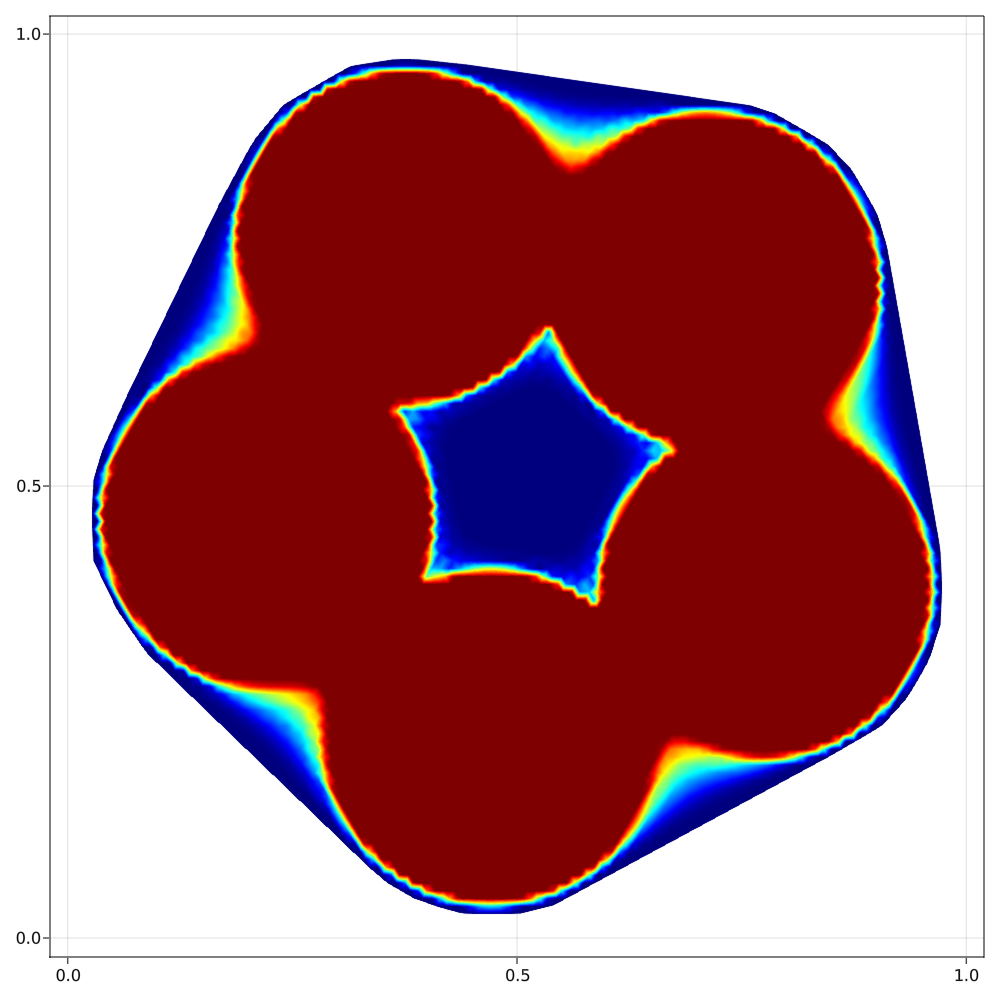

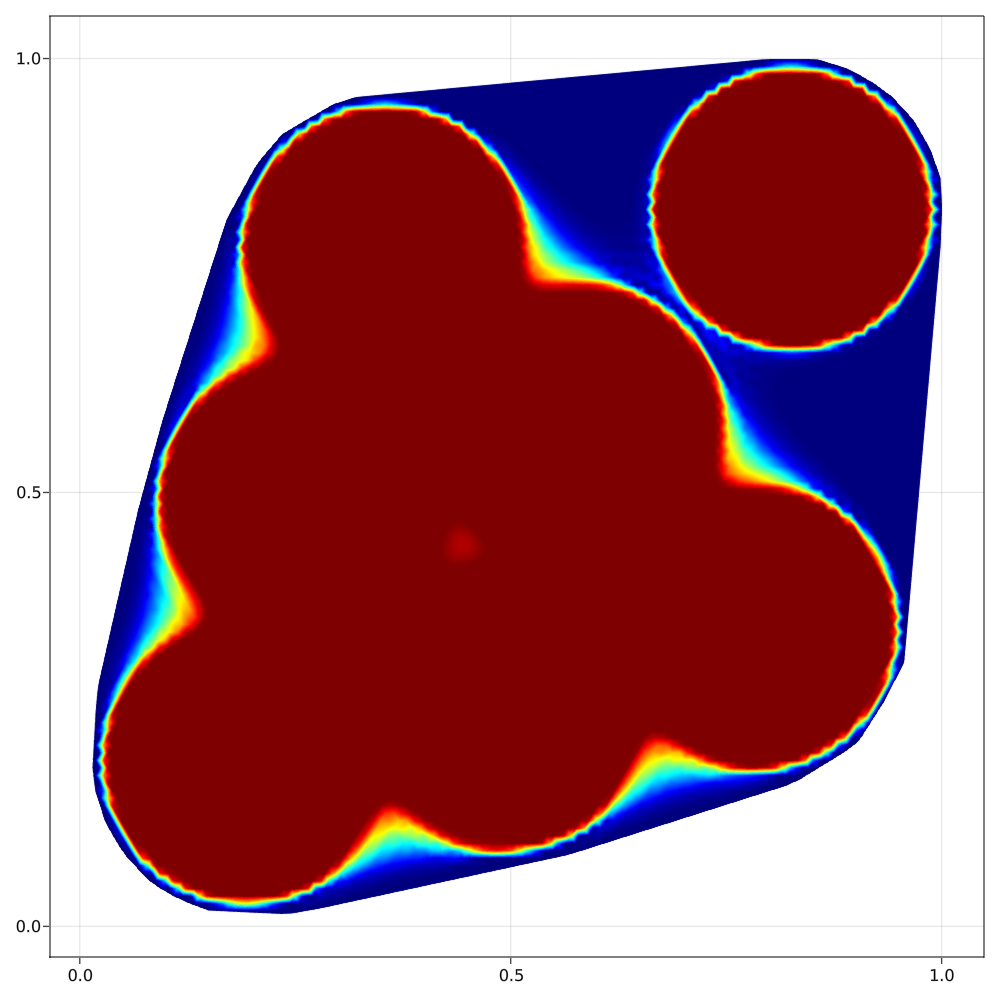
Companion articles :
-
Maximization of Neumann eigenvalues
(2023),
with D. BUCUR and E. OUDET,
Archive for Rational Mechanics and Analysis.